1-fix-3 die wirkliche Rendite berechnen (interner Zinsfuß leicht gemacht)

Wie kannst du eine Rendite pro Jahr für jede beliebige Geldanlage oder einen Mix daraus berechnen?

Das möchte ich in diesem etwas längeren Artikel erklären, und zwar so, dass du es verstehst und hinbekommst, ohne eine fette Formel auswendig lernen oder umformen zu müssen.

Der Schlüssel dazu ist der interne Zinsfuß.

Die Ausgangssituation

Du investierst mehrmals im Jahr zwischendrin in verschiedene Geldanlagen, manche davon haben einen vorgegebenen Zins, manche nicht.

Mal bekommst du Auszahlungen, egal ob sie Zinsen, Dividende oder Ausschüttung heißen. Manchmal werden Erträge automatisch wieder angelegt und damit weiter verzinst, manchmal auch nicht.

Manchmal verkaufst du eine Investition mit Gewinn oder auch mit Verlust. Dann werden noch Steuern abgezogen, die auch wieder ihren ganz eigenen Regelungen unterliegen.

Wie kannst du eine Rendite pro Jahr über alles ermitteln, also einen effektiven Jahreszins, den du mit deinen Geldanlagen erwirtschaftest?

Vielleicht möchtest du aber nur gezielt einen bestimmten Teil betrachten. Du möchtest z. B. wissen, wie viel Rendite pro Jahr dir dein Aktiendepot über einen gewissen Zeitraum gebracht hat.

Wenn du nach einer allgemeinen Lösung dafür suchst, stößt du auf die Begriffe: interner Zinsfuß, interne Rendite oder interner Zinssatz und wirst mit Dingen wie Kapitalwertformel und Nettobarwert bombadiert, die zum Verständnis der ganzen Thematik vorausgesetzt werden.

Dann folgt meistens eine kompliziert wirkende Formel, so dass Mathe-Allergiker gleich die Lust an der Sache verlieren und es auf sich beruhen lassen.

Aber keine Angst, das Ganze lässt sich einfacher erklären, als es üblicherweise getan wird. Ich werde es in diesem etwas längeren Artikel versuchen, ohne dich mit fetten Formeln, in denen viele Buchstaben vorkommen, zu quälen.

Zinsen rauf und runter rechnen

Verzinsen (Aufzinsen)

Beginnen wir mit einer Grundlagenbetrachtung, bei der wir die jährliche Rendite kennen. Sie soll 5 % pro Jahr betragen. Wir wissen, dass dann jeweils „100 € von heute“ zu „105 € in einem Jahr“ werden.

Der Prozess heißt Verzinsen oder Aufzinsen. Dazu müssen wir für jedes Jahr mit 1+Zinssatz multiplizieren. In unserer Betrachtung bei einem Zinssatz von 5 % = 0,05 multiplizieren wir jeweils mit 1,05.

Beginnen wir mit einem Betrag von 1.000 €. Nach einem Jahr werden daraus

1.000 € × 1,05 = 1.050 €

Nach einem weiteren Jahr:

1.050 € × 1,05 = 1.102,50 €

Nach noch einem Jahr:

1.102,50 € × 1,05 = 1.157,625 €

(1.157,62 €, da es bei €-Beträgen nur zwei Stellen nach dem Komma gibt.)

usw.

So geht das mit dem Zins und Zinseszins, also wenn die Zinsen drin bleiben und im folgenden Zeitraum mitverzinst werden.

Wir hätten auch gleich rechnen können:

1.000 € × 1,05³ = 1.000 € × 1,157625 = 1.157,625 €

Abzinsen – die andere Richtung

Schauen wir uns die andere Richtung an: Wir wissen, was wir am Ende haben wollen. Wie kommen wir dann auf den Betrag, den wir bei einer jährlichen Rendite von 5 % heute dafür aufbringen müssen?

Das geht genau umgekehrt. Wir teilen den Endbetrag für jedes Jahr durch 1+Zinssatz, hier also durch 1,05. Das nennt man Abzinsen. So etwas ist Verzinsung rückwärts.

Nehmen wir an, wir wollen in drei Jahren 1.000 € haben. Wie viel müssen wir heute dafür aufbringen? Wir rechnen dazu:

1.000 € ÷ 1,05³ = 1.000 € ÷ 1,157625 = 863,84 €

Das können wir überprüfen:

Aus 863,84 € werden bei 5 % jährlichen Zinsen nach einem Jahr

863,84 € × 1,05 = 907,03 €

Nach einem weiteren Jahr werden daraus

907,03 € × 1,05 = 952,38 €

Schließlich nach dem dritten Jahr

952,38 € × 1,05 = 1.000 €

Oder gleich so berechnet:

863,84 € × 1,05³ = 1.000 €

Das ist logisch, denn wir hatten ja die 1.000 € durch 1,05³ geteilt, um auf die Ausgangssumme von 863,84 € zu kommen.

Beträge ohne Zinseszins

Wie sieht es aus, wenn die Zinsen selbst nicht verzinst, sondern ausgeschüttet werden? So etwas kommt z. B. bei Immobilien-Crowdinvesting-Projekten vor. Hier der Anschaulichkeit halber etwas idealisiert:

Du investierst 1.000 € für genau drei Jahre. Immer zum Jahresende bekommst du dafür 5 %, also 50 €, ausgezahlt. Am Ende, also nach drei Jahren, bekommst du außerdem deine 1.000 € zurück.

Die Auszahlungen von jeweils 50 € nach einem bzw. zwei Jahren werden nicht weiter verzinst. Aber du könntest sie selbst wieder in eine Geldanlage stecken, die Rendite trägt.

Wenn wir wieder den Zinssatz von 5 % zugrunde legen, können wir ausrechnen, was 50 €, die wir in einem Jahr erhalten, heute wert sind, und zwar durch Abzinsen:

50 € ÷ 1,05 = 47,62 €

Dagegen sind 50 €, die wir erst in zwei Jahren erhalten, heute nur 45,35 € wert, denn

50 € ÷ 1,05² = 45,35 €

Der heutige Wert der 1.050 €, die wir in drei Jahren erhalten, also die letzte Zinszahlung über 50 € plus die ursprünglichen 1.000 €, ist bei einem jährlichen Zinssatz von 5 %, nur

1.050 € ÷ 1,05³ = 907,03 €

Rechnen wir diese drei abgezinsten Beträge zusammen, kommen wir auf

47,62 € + 45,35 € + 907,03 € = 1.000 €

Genau so soll es sein.

Die Zinsen aus Einzelbeträgen berechnen

Nun kommen wir zu dem, was wir eigentlich haben wollen. Wir kennen die Einzelbeträge und wollen daraus den zugrunde liegenden Zinssatz berechnen.

Als Fleißarbeit

Wir haben nur die Angaben, wann wir welchen Betrag (welche Beträge) investiert bzw. wann wir wie viel herausbekommen haben.

Wir wollen nun den dazugehörigen Zinssatz ermitteln.

Dabei versehen wir investierte Beträge mit einem Minus. Beträge, die wir heraus bekommen haben, mit einem Plus. Für unser Beispiel aus dem vorigen Abschnitt sieht das dann so aus:

Jahr	Betrag €	Erklärung
0	-1.000	1.000 € investiert
1	+50	50 € Zinsen erhalten
2	+50	50 € Zinsen erhalten
3	+1.050	50 € Zinsen und 1.000 € Rückzahlung erhalten

Wie lässt sich der jährliche Zinssatz, bei dem das so ist, daraus berechnen? (Wenn wir es nicht wüssten bzw. es nicht auf einen Blick sehen könnten.)

Wir suchen also eine Zahl x, für die gilt:

-1.000 + 50 ÷ (1+x) + 50 ÷ (1+x)² + 1.050 ÷ (1+x)³ = 0

Das ließe sich noch ein wenig umformen. Aber ich habe versprochen, hier niemanden mit Formeln zu quälen.

Im Normalfall ist die linke Seite der Formel noch viel komplizierter und würde mit einem allgemeinen Summenzeichen und Laufvariablen usw. ausgedrückt werden. Das brauchen wir hier nicht.

Die einfachste Möglichkeit, so etwas zu lösen, besteht im Ausprobieren. Dabei grenzt man den gesuchten Wert immer mehr ein.

Zum obigen sehr einfachen Beispiel geht das in etwa so:

Probiert man es mit 4 %, also x = 0,04, kommt folgendes heraus:

-1.000 + 50 ÷ 1,04 + 50 ÷ 1,04² + 1.050 ÷ 1,04³ = 27,75

Das geht prima mit Excel (oder Google Tabellen o. ä.):

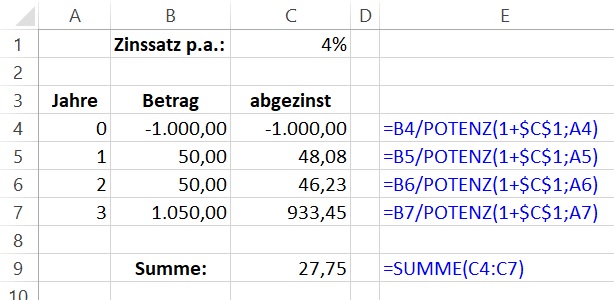
In Blau (ganz rechts) zeige ich die verwendeten Excel-Formeln.

Mit 4 % abzuzinsen genügt also nicht. Nehmen wir 6 %. In Excel braucht man das nur an einer Stelle auszutauschen:

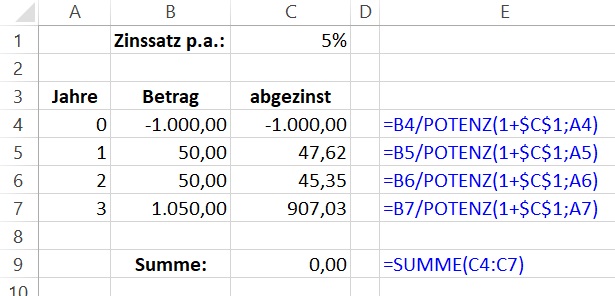
-1.000 + 50 ÷ 1,06 + 50 ÷ 1,06² + 1.050 ÷ 1,06³ = -26,73

Da wurde etwas zu viel abgezinst. Also probieren wir etwas zwischen 4 % und 6 % usw.

So kommen wir letzten Endes auf unsere 5 %.

Durch Excel den internen Zinsfuß noch einfacher berechnen

Das Schöne ist, dass Excel für genau so etwas (Berechnung des internen Zinsfußes) bereits eine fertige Funktion hat. Diese heißt IKV. So einfach funktioniert sie:

In Google Tabellen gibt es diese Funktion übrigens auch.

Sie macht intern nichts anderes als wir im vorigen Abschnitt. Sie probiert systematisch durch und grenzt den Zinssatz ein, bis er passt. Dazu braucht sie im Gegensatz zu uns nur einen Sekundenbruchteil.

Ob es sich bei den einzelnen Zinsperioden um ein Jahr oder jeweils eine andere Zeitspanne handelt, ist der Funktion egal. Als Argument erwartet IKV immer eine Liste von Zahlen, die mit dem zu ermittelnden Prozentsatz abgezinst werden sollen.

Die an erster Stelle angegebene Zahl wird nicht abgezinst, denn sie gilt zum Zeitpunkt 0, die nächste wird einmal abgezinst, die übernächste zweimal usw.

Die Prozentzahl, die dabei herauskommt, bezieht sich dann auf die Spanne zwischen jeweils zwei angegebenen Zahlen. Wenn wir monatliche Beträge angeben, kommt ein Zinssatz pro Monat heraus usw. Der kann dann auf ein Jahr hochgerechnet werden.

Wenn die Rechnung zu komplex wird, weil wir zum Beispiel alles auf einen Tag genau angeben, kommt bei der Excel-Funktion IKV ein Fehler (#DIV/0!) heraus. In dem Fall müssen wir der Funktion helfen, indem wir als zweites Argument einen geschätzten Startwert für die Berechnung angeben. Das muss nur ganz grob geschätzt sein. Dann kommt das richtige Ergebnis heraus.

Nun kommen Anwendungsbeispiele aus einem meiner Finanzexperimente, die das Ganze anschaulicher machen.

Beispiel 1

Nehmen wir einfach mal mein Experiment Immobilien-Crowdinvesting gegen ETF-Sparplan und betrachten daraus die bereits zurückgezahlten Immo-Projekte. Das sind bei mir vier Stück (Stand Mitte Oktober 2021). Wie groß ist die effektive Jahresrendite dieser Projekte im Schnitt?

Ich verwende für die Berechnung ganze Monate als Zeitspanne. Das ist genau genug.

Projekt 1: Jena Dornburger Straße
investiert im März 2020: 30 €
Zinszahlungen: Juli 2020: 0,36 €, März 2021: 1,07 €
Rückzahlung im März 2021: 30 €

Alles, was ich ausgebe, wird als Minusbetrag, alles, was ich bekomme, als Plusbetrag vermerkt.

In einer Tabelle dargestellt, sieht das für dieses Projekt so aus:

Monat	Beträge €
März 2020	-30
April 2020
Mai 2020
Juni 2020
Juli 2020	0,36
August 2020
September 2020
Oktober 2020
November 2020
Dezember 2020
Januar 2021
Februar 2021
März 2021	1,07	30

Die anderen drei abgeschlossenen Projekte werden nach dem gleichen Schema in die Tabelle übernommen.

Projekt 2: Pflegezentrum Boizenburg
investiert im April 2020: 30 €
Zinszahlungen: Juni 2020: 0,17 €, Juli 2020: 0,10 €, Juli 2021: 1,42 €, August 2021: 0,22 €, August 2021: 0,30 € (Bonuszins)
Rückzahlung im August 2021: 30 €

Projekt 3: Fellbach II
investiert im Mai 2020: 30 €
Zinszahlung: Dezember 2020: 0,63 €
Rückzahlung im Dezember 2020: 30 €

Projekt 4: Alte Glockengießerei Rüdersdorf
investiert im August 2020: 30 € (Stückzinsen gezahlt 0,28 €, da auf dem Handelsplatz gekauft)
Zinszahlungen: Dezember 2020: 0,70 €, März 2021: 0,22 €
Rückzahlung im März 2021: 30 €

Dann werden alle Einzelbeträge über die Monate aufsummiert, so dass es zu jedem Monat eine Zahl gibt. Wenn in einem Monat nichts passiert ist, ist 0 die Summe.

Über diese Gesamt-Zahlen wird dann mittels der Formel IKV in Excel der dazugehörige Zinssatz (interner Zinsfuß) ausgerechnet. Meistens ist dessen angezeigte Formatierung zu ungenau und sollte auf zwei paar Stellen hinter dem Komma angepasst werden.

Dieser Zinssatz ist jedoch der effektive Monatszins. Der lässt sich auf den effektiven Jahreszins umrechnen.

So sieht das Ganze in Excel aus:

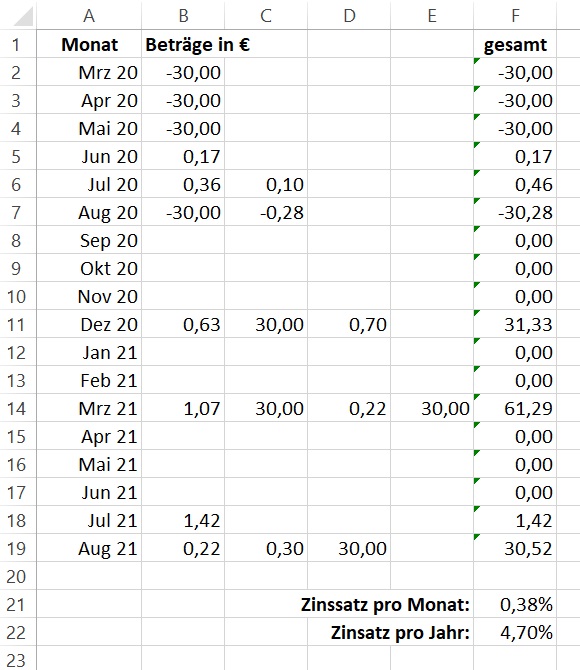
Für den Zinssatz pro Monat wurde die Funktion IKV auf die Liste der darüber stehenden Werte angewendet.

Wie kommt man vom Zinssatz pro Monat auf den Zinssatz pro Jahr?

Indem man die Frage beantwortet: Was wird aus einem Euro, wenn dieser zwölf Monate hintereinander mit dem Monatszins verzinst wird?

Man multipliziert einfach 1+Monatszinssatz, und zwar zwölfmal hintereinander. Anschließend zieht man den Euro wieder ab und hat den Betrag, der hinzugekommen ist. Schon hat man den effektiven Jahreszins.

Die Excel-Formel dafür ist:

=POTENZ(1+F21;12)-1

und als Prozent formatieren, wobei in F21 der Monatszins steht.

Das Ergebnis zu Beispiel 1:

Effektiv sind also bei meinen abgeschlossenen Immo-Crowdinvesting-Projekten bisher etwa 4,7 % jährliche Rendite herausgekommen. Die Steuerabzüge sind darin schon berücksichtigt.

Beispiel 2

Bleiben wir beim Immo-Crowdinvesting aus meinem Experiment. Ich betrachte jedoch nicht die einzelnen Projekte und deren Ausschüttungen, sondern die Crowdinvesting-Seite als Ganzes („Black Box“).

In diese Kiste habe ich seit Oktober 2019 Monat für Monat jeweils 30 € gesteckt und niemals Geld herausgenommen. Ich betrachte die Sache mit der Vereinfachung, dass ich die Projekte (jetzt, im Oktober 2021) alle zu 100 % Nennwert an jemand anderen verkaufen könnte.

Dazu würde ich noch die jeweils bis dahin aufgelaufenen Stückzinsen vom Käufer erhalten. Die Handelsplatzgebühr lasse ich weg, denn es gibt Freetrades.

Dann würde meine Übersicht zu den Zahlungsströmen so aussehen:

Monat	Betrag in €
Oktober 2020	-30
November 2020	-30
…	…
August 2021	-30
September 2021	-30
Oktober 2021	650 + 14,09 + 100,68 = 764,77

Zur Erklärung der letzten Zeile: 650 € ist der Nennbetrag meiner Crowdinvesting-Projekte zusammen. 14,09 € sind die aufgelaufenen Stückzinsen. 100,68 € ist der Bargeldbestand.

Lassen wir hier wieder mittels Excel-Funktion IKV den Effektivzins pro Monat und daraus den effektiven Jahreszins ausrechnen:

Hier kommen sogar etwa 5,9 % pro Jahr heraus. Also mehr als bei meinen vier abgeschlossenen Projekten. Wie kann das sein?

Zum einen sind die 10 € Neukundenbonus der Immo-Plattform BERGFÜRST* enthalten und von den aufgelaufenen Stückzinsen wurden keine Steuern abgezogen.

Rechnen wir beides heraus, ziehen also vom Bargeldbestand 10 € ab und reduzieren die Stückzinsen auf knapp drei Viertel, kommen nur noch knapp über 4 % pro Jahr heraus.

Das ist plausibel, denn es gibt immer einen Bargeldanteil, der unverzinst „herumliegt“. So muss in dieser Betrachtung eine etwas kleinere Rendite herauskommen als im vorigen Beispiel, in dem nur die abgeschlossenen Projekte berücksichtigt wurden.

Beispiel 3

Im Vergleich dazu, die auf die gleiche Art und Weise ausgerechnete Jahresrendite der anderen Seite im Experiment. Dabei handelt es sich um Investition in einem ETF-Sparplan in Immobilienaktien und REITs.

Auch das betrachte ich als „Black Box“. Die Einzahlungen in diese Kiste sind die gleichen wie beim Immo-Crowdinvesting, also jeweils 30 € von Oktober 2019 bis September 2021. Die werden jeweils mit einem Minus davor berücksichtigt.

Nun brauche ich nur den Wert der Anteile plus den Bargeldbestand auszurechnen und diesen Betrag für jetzt (Oktober 2021) einzutragen. Das sind zusammen 851,05 €.

Die gleiche Rechnung wie im vorigen Beispiel ergibt einen effektiven Jahreszins von 16,9%.

Zugegeben, das ist etwas zu hoch angesetzt. Wenn ich alle Anteile jetzt verkaufen würde, gingen noch Steuern auf den realisierten Kursgewinn ab. Das wären etwa 33 €. Also bleibt ein Betrag von rund 818 €. Damit würde eine effektive Jahresrendite von 12,8 % herauskommen.

Über eine längere Distanz wird die jährliche Rendite ganz sicher nicht so hoch bleiben. Das ist hier deshalb so, weil es zwischendurch ein „Tal der Tränen“ gab, wo durch den Sparplan immer wieder günstig eingekauft werden konnte.

Zusammenfassung – die Berechnung deiner Effektivrendite Schritt für Schritt

Wie beschrieben kannst du nun für alles, was du willst, die Renditen berechnen. Welche Investments du dabei wie einbeziehst, kannst du selbst wählen.

Ich denke, ich habe dir damit ein relativ einfaches, aber dennoch mächtiges, Werkzeug gezeigt.

So verwendest du es Schritt für Schritt:

Schritt 1: Zeitraster festlegen

Entscheide zunächst, welche Zeitspanne du jeweils zwischen den einzelnen Datenpunkten betrachten möchtest, z. B. ein Jahr, einen Monat oder sogar einen Tag und lege dir eine entsprechende Excel-Datei an.

Schritt 2: Alle Daten (Geldströme) eintragen

Ordne alle deine Bewegungen innerhalb des Investments mit dem richtigen Vorzeichen in dieses Raster ein.

Schritt 3: Summen bilden

Addiere dann zu jedem Zeitpunkt die dazugehörigen Beträge. Wenn es zu einem Zeitpunkt keine gibt, steht dort einfach 0.

Schritt 4: IKV-Funktion anwenden

Berechne über die Liste dieser Gesamtbeträge mittels der Excel-Funktion IKV (für den internen Zinsfuß) den Effektivzins für dein Zeitraster (ein Jahr, ein Monat, ein Tag).

Schritt 5: Umrechnen auf ein Jahr

Rechne auf den effektiven Jahreszins um.

Fertig!

Was noch offen ist

Wofür genau die einzelnen Buchstaben in IKV stehen, weiß ich nicht. Wenn du es weißt oder einen Vorschlag hast, schreib mir einen Kommentar.

Wenn du Fragen dazu hast, oder einen Fehler in meiner Darstellung entdeckst – ich bin schließlich auch nur ein Mensch –, schreib mir bitte auch einen Kommentar dazu.

Mit * markierte Links sind Affiliate-Links. Über jeden Abschluss darüber erhalte ich eine kleine Provision, die dich nichts extra kostet. Du kannst solche Links hier suchen. Ich möchte mit Absicht meinen Inhalt nicht mit so etwas zupflastern, genauso wenig, wie ich dir meine Newsletter-Anmeldung wie einen nassen Waschlappen ins Gesicht klatsche (siehe: Geld verdienen im Internet: Von Newslettern und Waschlappen).