Mit der 72er-Regel Zinsen super einfach berechnen

Mathe ist nicht so deins? Aber Zinsen berechnen zu können wäre schon cool? Denn du möchtest wissen: Nach welcher Zeit verdoppelt sich dein Kapital bei vorgegebenem Zinssatz? Oder anders herum: Welchen Zinssatz pro Jahr brauchst du, um dein Kapital in vorgegebener Zeit zu verdoppeln? Mit der 72er-Regel kannst du das ohne viel Hirnschmalz herausbekommen.

Zinsen berechnen bis zur Verdopplung – der „normale“ Weg

Nehmen wir an, du hättest etwas gefunden, das 6 % Rendite pro Jahr bringt. Wenn dein Kapital also Jahr für Jahr um diese 6 % wächst, wie lange würde es dann dauern, bis es sich verdoppelt?

Wenn du 6 % auf einen Betrag draufrechnen möchtest, multiplizierst du diesen einfach mit 1,06. Für ein weiteres Jahr rechnest du wieder „mal 1,06“ usw.

Du kannst also in einen Taschenrechner, z. B. vom Smartphone, eintippen:

1,06 × 1,06

Dann drückst du mehrmals hintereinander auf „=“. Dadurch wird immer wieder mit 1,06 multipliziert und das jeweilige Ergebnis angezeigt.

Du drückst nun sooft hintereinander auf „=“, bis etwas um die 2 als Ergebnis erscheint, und du zählst bei jedem Druck auf „=“ mit. So viele Jahre dauert es bis zur Verdopplung.

Eintippen: 1,06 × 1,06

= drücken und zählen „2“: 1,1236

= und „3“: 1,191016

= und „4“: 1,26247696

usw.

= und „12“: 2,0121964718

Fertig!

Bei einer Rendite von 6 % p. a. („p. a.“ = „per anno“= „pro Jahr“) dauert es also 12 Jahre, bis sich das Anfangskapital verdoppelt hat.

Das geht jedoch viel einfacher, und zwar im Kopf. Und dazu musst du nur leidlich Kopfrechnen können.

Der Trick ist die 72er-Regel, manchmal auch 72er-Formel genannt

Die besagt: Wenn du bei vorgegebenem jährlichen Zinssatz wissen möchtest, wie viele Jahre es in etwa dauert, bis sich dein Kapital verdoppelt, teile einfach 72 durch den Zinsfuß. Der Zinsfuß ist einfach die Zahl vor dem Prozentzeichen.

In unserem Beispiel bei einem Zins von 6 % p. a.:

72 : 6 = 12

So bekommst du das gleiche Ergebnis – nämlich 12 Jahre – viel schneller heraus.

Diese Vereinfachung ist natürlich nur eine Annäherung. Aber für Zinssätze etwa zwischen 1 % und 15 % ist die ziemlich genau.

Warum funktioniert das?

Auf die mathematische Herleitung verzichte ich an dieser Stelle, denn sie ist im Wikipedia-Artikel zur 72er-Regel recht gut erklärt.

Eigentlich kommt dabei anstelle der 72 etwas zwischen 69 und 70 heraus. Man könnte also auch die 69 oder 70 durch den Zinsfuß teilen, um dann in etwa die Dauer bis zur Verdopplung herauszubekommen.

Besonders für sehr kleine Zinssätze ist die Berechnung mit 69 oder 70 etwas genauer. Aber wen interessieren schon Zinsen nahe der 0 %? Da kommt es im Ergebnis auf hundert Jahre mehr oder weniger auch nicht an.

Die 69er-Variante wird sogar für eine breitere Spanne von Zinssätzen exakter, wenn man nach dem Teilen durch den Zinsfuß noch einen kleinen Wert – meistens 0,35 oder 0,32 – addiert. Aber das ist dann keine sehr einfache Kopfrechenmethode mehr.

Die 72 wird verwendet, weil es sich meistens viel besser rechnet, besonders bei ganzzahligem Zinsfuß, denn 72 hat viele Teiler. Bei den „gängigen“ Zinssätzen wird das dadurch nicht sehr viel ungenauer.

Die 72er-Regel funktioniert auch anders herum

Das Schöne ist, dass sich die 72er-Regel auch umgekehrt anwenden lässt. Damit ist gemeint, dass du anstelle des Zinssatzes auch die Dauer bis zur Verdopplung des Kapitals vorgeben kannst, um daraus den benötigten Zinssatz zu berechnen.

Beispiel:

Du möchtest, dass sich dein Kapital innerhalb von 8 Jahren verdoppelt. Wie hoch muss der dazugehörige Zinssatz sein?

Auch dazu kannst du einfach 72 durch die Dauer in Jahren teilen und bekommst als Ergebnis den gesuchten Zinsfuß.

72 : 8 = 9

Du brauchst also eine Rendite von etwa 9 % pro Jahr, damit sich dein Kapital nach 8 Jahren verdoppelt.

Das lässt sich leicht nachprüfen:

1,09 × 1,09 × … × 1,09 (8mal hintereinander)

oder

1,09 „hoch“ 8

= 1,9925626417

Das ist in etwa 2. Stimmt also mit rund 9 %.

Noch eine Anwendung: Aktienmarkt-Rendite schätzen durch Draufschauen und 72er Regel

Du kannst damit ohne viel zu rechnen nachprüfen, wie sich der globale Aktienmarkt (der Industriestaaten) langfristig im Schnitt pro Jahr etwa entwickelt hat.

Nehmen wir dazu den MSCI World Gross Total Return Index. Dieser spiegelt die Entwicklung der Aktienmärkte der industrialisierten Welt ganz gut wider und berücksichtigt dabei sowohl Kursentwicklung als auch Dividenden.

Bei onvista findet man dazu folgenden Chart.

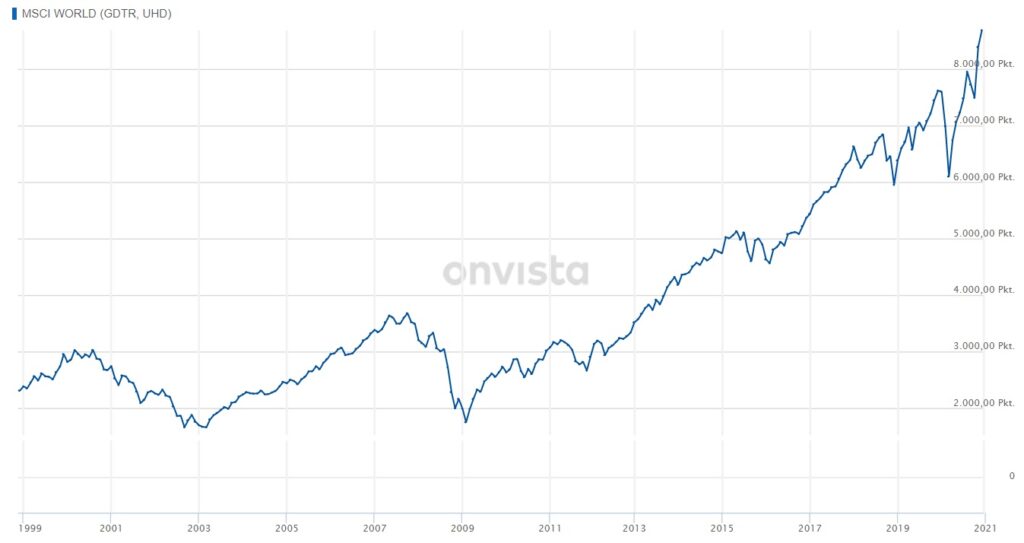
Durch Darüberfahren mit der Maus (nicht hier, sondern bei onvista) lässt sich ablesen, dass der Anfangswert dieser Darstellung im Dezember 1998 rund 2.300 Punkte betrug und der Wert im Dezember 2020 bei rund 8.689 lag.

Das ist mit Augen und Hühneraugen zudrücken fast eine Vervierfachung. Das heißt es wurde über einen Zeitraum von 22 Jahren zweimal verdoppelt. Bei dem gesuchten Zinssatz sollte eine Verdopplung damit jeweils nach 11 Jahren eintreten.

Nehmen wir nun die 72er Regel. Dabei brauchen wir nicht genau zu rechnen, denn das mit den Verdopplungen war ja auch nicht genau.

72 geteilt durch 11 ist irgendetwas zwischen 6 und 7.

Also wird ein Zinssatz zwischen 6 % und 7 % herauskommen, eher in der Nähe von 6 %, da das mit der Vervierfachung, also der zweimaligen Verdopplung, ja nur „fast“ der Fall war.

Ist das seriöse Mathematik? Nö, aber für die Praxis reicht’s und es ging sehr schnell.

Rechnen wir genauer nach:

Teilen wir den Endwert vom Dezember 2020 durch den Anfangswert vom Dezember 1998:

8.689 : 2.300 = 3,7778

Der Wert hat sich also ver3,7778facht.

Das hat 22 Jahre gedauert. Wir möchten nun die Zahl wissen, die 22mal miteinander multipliziert, 3,7778 ergibt. Das ist die 22te Wurzel aus 3,7778, oder 3,7778 „hoch“ 1/22.

Excel kann das im Handumdrehen mit der Funktion „POTENZ“ ausrechnen.

Das Ergebnis: 1,0623

So sieht das in Excel aus:

Der Startwert 2.300 muss also 22mal hintereinander mit rund 1,0623 multipliziert werden, um den Endwert 8.689 herauszubekommen.

Das entspricht einer Verzinsung von 6,23 % jährlich.

Das ist keine Überraschung.

Bringt die genaue Kenntnis der Stellen nach dem Komma nun irgendeinen Mehrwert? Ich denke nein, vor allem wenn man die echten Wertschwankungen betrachtet.

Im Endeffekt wird man bei Renditen in diesem und höherem Bereich schon aufgrund des Risikos keine langfristige Gleichmäßigkeit finden.

Hinzu kommt dann noch die Sache mit den Steuern und dann ist da noch die Inflation, also die Tatsache, dass 100 € heute von der Kaufkraft her nicht das Gleiche sind wie 100 € in ein paar Jahren. Aber lassen wir das.

Fazit

Die 72er-Regel reicht für die Praxis vollkommen aus, und zwar um

• bei vorgegebener Rendite den Zeitraum bis zur Verdopplung des Kapitals zu ermitteln
• oder bei vorgegebenem Zeitraum die benötigte Rendite zu „berechnen“

Einfach 72 durch das eine teilen und das jeweils andere kommt in etwa heraus.

Mehr zur Renditeberechnung?

Wenn du wissen möchtest, wie du eine auf jeweils ein Jahr umgerechnete Effektivrendite für nahezu jede Geldanlage berechnen kannst, empfehle ich dir meinen nächsten Artikel.